西湖论剑GlobalNoise[AI对抗启蒙]

近期CTF赛事里面AI对抗题出现频率逐渐升高，作为一个摸了好久的web人，正好之前自己有一点MachineLearning的基础，准备尝试一下这个领域

西湖论剑GlobalNoise[AI对抗启蒙]

2022/01/16补充：发了关于全连接神经网络的文章，手搓了一个模型之后再回来看这篇文章，发现很多地方有失偏颇(已基本修正)，正好之前有一个想把样本偏移到任意class的心愿没有完成，后续会发一篇新的文章L2 Targeted Attack

本文面向的对象是：

  • 对Machine Learning原理有基本理解的入门AI人
  • 吃瓜群众

（机器学习相关的前置知识建议看吴恩达，然后不调库自己写一点逻辑回归线性回归的基本分类器就够了（至少我在这之前只有这点基础，技术拉跨

题面

概述：提供了一个训练好的model和一份mnist数据集，要求对其中的100份样本进行一个全局性的较小扰动（对向量的范数进行了限制），使得这100份样本的分类正确率低于5%

下载链接(github源)

（当时没有存题面啊啊啊啊啊啊啊啊啊啊啊啊啊，并非完整原题，只是我根据回忆和需要的条件摸出来的一个题面

题面分析

将题目给出的100个样本过一个目会发现是7和9的______

如果你想的是二分类就不对了，因为是不可能用一个噪音把大部分7糊弄到9，然后把大部分9糊弄到7的（好多人一看到都说二分类

本来就是有10个类别（0~9），可以把9和7糊弄到除他俩之外的classes里面去

此题很明显关键在于Global，也正是这个Global和对范数的限制拦住了很多像我这样的半吊子

之前做过0CTF-final中的boyNextDoor，是一个人脸识别的题，正解是用梯度构造noise，还需要Expectation over Transformation (EOT) 来绕过dlib的随机抖动，当时属于是无知者无畏，直接随机改单像素给爆出来了，由于只需要构造人脸图片，所以对于噪音范数和噪音鲁棒性没有要求，只要他能识别到人脸位置即可

但是当我想在这个题用半吊子手法去解决时，很明显在范数限制和鲁棒性上都遇到了问题，通常来说根据梯度构造的噪音会比满足条件的随机噪音的L2(模长)小10~100倍，而且随机噪音只对单个样本有效，完全不能Global

所以人还是要进步，必须得理解正确构造噪音的方法

一篇论文

这是一篇关于全局扰动的文章，看一半大概就能知道构造全局扰动的原理了，其实也qs不难理解，但可能需要先理解模型的训练过程以及使用

  • 在训练时：这个过程就是在寻找一个最优的 线性(or非线性?) 的变换，使得输入经过这个变换之后能够落到集中的位置，这样就可以根据一些界限(决策边界)来划分的输入，并给出模型的判断

  • 在预测时：输入/数据 交给一个训练好的模型进行分类的时候，其实也就进行了一个映射，比如此处的mnist数据集是28x28的图片，那其实就是长度为784的向量，假设模型是f，那么f(x)就是模型对输入向量x预测的分类结果

  • 决策边界：其实在我个人目前的理解中，决策边界其实就指

    在这个闭合的边界内，所有落到这里面的f(x)都会被判定为某一个分类

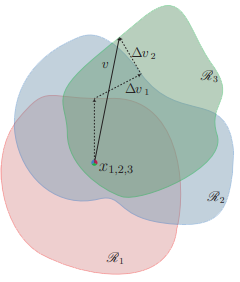
所以现在再回来看文中的图：

他描述的其实就是：

  • 在红，绿，蓝，三个决策边界内（二维扁平化的决策空间只是为了方便演示和理解），分别有三个样点x1（在红色边界内）,x2（在蓝色边界内）,x3（在绿色边界内）
  • 为了视觉上方便理解，把这三个点以及他们的决策空间重合在一起（原本的决策空间绝一般不会相互重叠，因为边界上正是预测结果改变的临界处，如果有一个模型存在太多这样的临界状况，那说明他这个模型不太行）
  • 对f(x)，使用梯度下降法，获取一个noise，这个noise可以最快地把x1送到红色的决策边界
  • 这时noise可以把原本落在红色这个决策空间内的x1直接送出到决策边界外去，但对于蓝色决策空间中的x2来说则不太好说
  • 故重复这一过程，但x2应更新为x2+=noise，对更新后的x2求一个能把x2送出决策边界的新noise，然后更新noise为noise+=newNoise
  • 对x3重复这一过程

这样就获得了一个可以把x1,x2,x3都送出决策空间的噪音（当然，求这个噪音的顺序会对最终得到的噪音有影响

具体实现

预处理

原题中的预处理是调库直接用的接口，我因为没有接触过太多机器学习的库所以手动处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import tensorflow as tf
from tensorflow import keras
import numpy as np
from PIL import Image
from numpy.linalg import norm
import matplotlib.pyplot as plt
import copy

model = keras.models.load_model('model.h5')
test_set=[13616, 4189, 3206, 51839, 30560, 45045, 51389, 59638, 10487, 5233, 48889, 10247, 1547, 3914, 44182, 9990, 26276, 28283, 52481, 46609, 18757, 26954, 26322, 18819, 29463, 34489, 51248, 53986, 25872, 42855, 49719, 31176, 38292, 48100, 52763, 3904, 46879, 9810, 51583, 39760, 21245, 13728, 33834, 23968, 28781, 33134, 35277, 18562, 21344, 8396, 36000, 43427, 24477, 36678, 56218, 32945, 17707, 36763, 611, 12668, 31312, 28053, 35696, 9876, 33329, 56107, 19929, 35636, 21704, 35807, 28645, 16522, 15192, 43890, 14710, 11805, 4754, 33660, 13270, 25465, 20267, 4141, 40391, 14287, 15545, 56458, 6121, 19663, 15709, 52825, 25933, 4091, 17861, 37773, 22450, 8669, 4447, 22022, 40046, 32738]

dict_mnist = np.load("mnist.npz")
x_train = dict_mnist["x_train"]
y_train = dict_mnist["y_train"]
x_test = dict_mnist["x_test"]
y_test = dict_mnist["y_test"]
dict_mnist.close()
x_train = np.expand_dims(x_train, axis=3)
x_test = np.expand_dims(x_test, axis=3)
#normalize
x_train = (x_train-np.amin(x_train))/(np.amax(x_train)-np.amin(x_train))
x_test = (x_test-np.amin(x_test))/(np.amax(x_test)-np.amin(x_test))

test_x_data = []
test_y_data = []
for i in test_set:
    test_x_data.append(x_train[i])
    test_y_data.append(y_train[i])
test_x_data = np.array(test_x_data)
test_y_data = np.array(test_y_data)
test_x_data = test_x_data.astype(np.float32)
test_y_data = test_y_data.astype(np.float32)

获取梯度

tensorFlow提供了很好用的求梯度的接口gradientTape

2022/01/16补充：这个函数在之前写wp的时候对我来说就是一个黑盒，对模型求输入的梯度的具体原理请看开头提到的新文章

1
2
3
4
5
6
7
8
9
10
11
12
def GetGrad(data, classIndex=-1):
    # 当 classIndex=-1，求样本到最近的最高概率点
    # 当指定 classIndex，求样本到指定的classIndex的最高概率点
    data = data.reshape(-1, 28, 28, 1)
    data = tf.cast(data, tf.float32)
    with tf.GradientTape() as tape:
        tape.watch(data)
        pred = model(data)
        # loss = tf.norm(pred, axis=1, ord=2) if classIndex == -1 else pred[0][classIndex]  # 有的文章把loss这么写
        loss = pred[0][np.argmax(pred)] if classIndex == -1 else pred[0][classIndex]
    grad = tape.gradient(loss, data)
    return np.array(grad).reshape(28, 28, 1)

梯度下降求noise

这样求出来的noise通常能以最小的Lp将样本送出去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def GradDes(data, foolRate=0.5, step=0.05, maxIteration=500):
    minGrad = 0.05
    arg = np.argmax(model.predict(data.reshape(-1, 28, 28, 1)))
    print("GetPert init arg : " + str(arg))
    cnt = 0
    pert = copy.deepcopy(data / np.inf)
    while True:
        cnt += 1
        rate = model.predict(data.reshape(-1, 28, 28, 1) + pert.reshape(-1, 28, 28, 1))[0][arg]
        print("\r - Iteration : " + str(cnt) + " rate : " + str(rate), end = '')
        if rate < foolRate or cnt == maxIteration:
            result = model.predict(data.reshape(-1, 28, 28, 1) + pert.reshape(-1, 28, 28, 1))[0]
            print("\n - pert result : " + str(np.argmax(result)) + " : " + str(np.amax(result)))
            break
        grad = GetGrad(data + pert)
        if norm(grad) < minGrad:
            if norm(grad) == 0:
                print("ERROR: grad is zero")
                break
            grad *= minGrad / norm(grad)
        pert -= grad * step
    return pert

main

这样求算数平均值得方法其实有点问题，如果恰好有一个反向的pert，那不直接抵消哩，而且我用到的样本里面还有一个是一开始本来就被分类器误分类的点= =...但是既然他得出的结果能用那就先在这里这么写，然后再讨论更好的解法嗯

用了算数平均值来求noise，没有鲁棒性

1
2
3
4
5
6
7
8
9
10
pert = [0] * 6
for i in range(3):
    pert[i] = GradDes(test_x_data[np.argwhere(test_y_data == 9)[i][0]])
    pert[i] = GradDes(test_x_data[np.argwhere(test_y_data == 7)[i][0]] + pert[i])
    pert[2 * i] = GradDes(test_x_data[np.argwhere(test_y_data == 7)[2 * i][0]])
    pert[2 * i] = GradDes(test_x_data[np.argwhere(test_y_data == 9)[2 * i][0]] + pert[2 * i])
pertSum = pert[0]/np.inf
for i in pert:
    pertSum += i
pert = pertSum/6

exp优化

目前的想法是：最好是通过求：将样本带到不同的边界的noise（比如本题中就是求出将样本7和9带到0,1,2,3,4,5,6,8的noise），然后比较这些noise在方向与范数上的差异，获得最优的noise，此时求算数平均值就没有问题了

但是在具体实现上遇到的问题就是：在梯度上升求noise的时候会陷入局部最优解（尤其是相差较大的class），然后目前虽然知道什么退🔥遗传🐜群啥的，但还没有想过具体到底怎么弄

但：对每一个class都求一个noise，使得某一特定样本偏移到其他的任意class是可行的

2022.4.6补充：根据最近了解的信息看来，陷入局部最优解大部分原因是因为卡在鞍点，换成更好的优化算法，如Adam等即可

Comments

⬆︎TOP